Module 6—Work and Energy
 Explore
Explore
Power
In the previous simulation, you will have noticed that when the lift is operating at any speed, the riders are gaining gravitational potential energy as soon as they are loaded at the bottom. Recall that a rider’s gain in gravitational potential energy is equal to the work done against the conservative force of gravity. Since the lift is not a closed system, energy will also be needed to overcome non-conservative forces, such as friction. Therefore, the work done by a chairlift can be defined as follows:
work done = energy to overcome conservative forces + energy to overcome
non-conservative forces
W = Ep + Elost
power: the rate of doing work
If you assume that the Elost due to non-conservative forces, such as friction, is constant, regardless of the speed at which the chairlift operates, is the work done by the lift constant, regardless of how fast it moves? If Ep and Elost are constant for a given mass, regardless of the speed at which it moves, the work done is not related to its speed. The power required to do the work at different speeds, however, does change. In the previous simulation, you should have noticed that when the lift operates at a high rate of speed, it consumes more power. What this means is that it does the same amount of work in lifting each rider of equal mass, but it does it faster and, in the process, consumes more power. Therefore, power is defined by the amount of work done in a given time interval.
Expressed as an equation, power is
![]()
| Quantity | Symbol | SI Unit |
| power | P | W |
| work | W | J |
| change in time | t | s |
1 W = 1 J/s of work. The unit of power was named in recognition of the scientific contributions of James Watt. Another common reference to power is “horsepower” (1 hp = 746 W).
Why does the chairlift require more power to move faster? You can answer this mathematically by substituting the equation for work into the power equation and then rearranging and simplifying it.
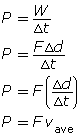
Therefore, you can see that if the conservative and non-conservative forces are constant, increasing the power acting on the system will cause an increase in the average speed of the system.
 Read
Read
Read “Power, Work, and Time” on pages 324 and 325 of the textbook to see examples of these concepts being used.
 Self-Check
Self-Check
SC 1. Complete question 1 of “Practice Problems” on page 325 of the textbook.
 Self-Check Answers
Self-Check Answers
SC 1.
Given
m = 1.50 t
h = 65.0 m
t = 3.50 min
Required
the power in watts and hp (P)
Analysis and Solution
The work done by the engine of the crane increases the gravitational potential energy of the mass. Convert the mass to kilograms and the time to seconds as part of the calculations in the equations.

Paraphrase
The power of the engine is 4.55 kW or 6.11 hp.
 Module 6: Lesson 4 Assignment
Module 6: Lesson 4 Assignment
Remember to submit the answer to TR 1 to your teacher as part of your Module 6: Lesson 4 Assignment.
 Try This
Try This
TR 1. A garage door opener is rated at 373 W. How much work can it do in 14.0 s of operation?
 Read
Read
What if a power question gives speed instead of time? Read “Power and Speed” on pages 327 to 329 in your textbook to see the answer.
 Self-Check
Self-Check
SC 2. Complete question 3 of “Practice Problems” on page 328 of the textbook.
 Self-Check Answers
Self-Check Answers
SC 2.
Given
m = 1250 kg
vi = 0.00 m/s
vf = 30.0 m/s
t = 4.00 s
Required
the power output of the motor (P)
Analysis and Solution
The work done is to accelerate the car, so calculate the acceleration and use Newton’s second law to calculate the force required. Then use
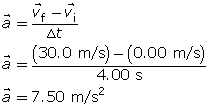
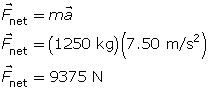
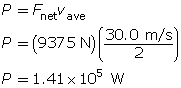
Paraphrase
The power output of the motor is 1.41 × 105 W or 141 kW.
 Module 6: Lesson 4 Assignment
Module 6: Lesson 4 Assignment
Remember to submit the answers to TR 2 and TR 3 to your teacher as part of your Module 6: Lesson 4 Assignment.
 Try This
Try This
TR 2. An automobile engine exerts a force of 595 N to propel the car at 90.0 km/h on a level road. What is the power output of the engine at that time?
TR 3. A traditional, double-seat chairlift can move 1200 people per hour (with an average mass of 60.0 kg) up a ski hill. A high-speed quad chair can move 2400 people in 30.0 minutes up the hill. If the upper terminal is 100 m higher than the lower terminal, how much power would each type of lift need just to overcome the force of gravity? Explain why they would need more power than the amount used to overcome the force of gravity.
Efficiency
Could a high-speed chairlift do more work using the same energy as the slower, older chairlift consumed? If so, it would be considered more efficient. In other words, less of the work done by the lift would be wasted by non-conservative forces (Elost) while still providing the same amount of energy for overcoming the conservative forces (Ep).
efficiency: the ratio of the output (useful work) to the input (total energy used)
Expressed as an equation, it is
![]()
Since the input and output occur in the same time interval, efficiency can be determined using either power or energy.
To determine the efficiency of the chairlift, you must first identify the input and output energy for the chairlift. Recall that the work done by the lift is transferred to the potential energy of the riders and the energy lost due to non-conservative forces such as friction. Therefore, Win = Ep + Elost.
In this equation, W is the work done by the lift—the energy input—and Ep is the conserved gravitational potential energy—the output. Therefore, efficiency could be described as follows:
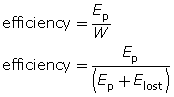
From this equation, you can see that if Elost is reduced, efficiency will increase. Perfect efficiency would only be achieved if Elost becomes zero, which is the case in a closed system (where all the work done becomes mechanical energy). The chairlift, however, is an open system, so it has less than 100% efficiency. If you assume that the lost energy (Elost) is nearly the same, regardless of speed, both the slow and fast chairlifts have identical efficiency.
So what is the net effect of increasing the speed of a chairlift? If the high-speed lift is just as efficient as the slow-speed lift, why does the high-speed lift use more power? On each type of lift, Elost is assumed to be identical, regardless of the speed. If the high-speed chair consumes more power in a time interval, the extra work done by the high-speed lift results in a greater amount of gravitational potential energy. But how can you have more potential energy without going farther up the hill? The answer is, move more mass. If the high-speed and low-speed lifts operate at capacity for the same time interval, the high-speed lift will have moved much more mass up the hill.
Increasing the speed of the chairlift will require more power and will move more riders per day when operating at capacity. The required power is purchased, which increases the costs of operating the ski hill. Additional lift-pass sales or an increase in the cost per pass (or both) would be required to support paying for the lifts capable of higher speeds, but patrons would be able to spend more time skiing and less time sitting or waiting in line.
 Self-Check
Self-Check
SC 3. What is the efficiency of a lift that uses 5.1 kW of power to move 24 people of average mass 60 kg a vertical distance of 80 m in 15 min?
 Self-Check Answers
Self-Check Answers
SC 3.
Given
Pin = 5.1 kW
m = (24 × 60 kg)
h = 80 m
t = 15 min
Required
the efficiency of the lift
Analysis and Solution
Calculate the power output; then calculate the efficiency.
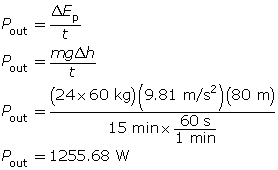

Paraphrase
The efficiency of the lift is 25%.
 Module 6: Lesson 4 Assignment
Module 6: Lesson 4 Assignment
Remember to submit the answer to TR 4 to your teacher as part of your Module 6: Lesson 4 Assignment.
 Try This
Try This
TR 4. Complete question 6 of “6.4 Check and Reflect” on page 330 of the textbook.