Module 6—Work and Energy
Explore
You will recall from Module 6: Lesson 2 that when a skier descends or comes down from the top of the mountain, gravitational potential energy is converted to kinetic energy—eventually, all the mechanical energy is lost due to friction. At the bottom of the hill, when standing still, the mechanical energy of the skier is zero relative to the mechanical energy he or she had at the top of the hill. This means that mechanical energy is not conserved; therefore, energy must be added in order to continue skiing once the skier reaches the bottom of the hill. Enter the chairlift.
When the skier gets back on the chairlift at the bottom of the mountain, work is done by the lift against the force of gravity as it moves back up the mountain. Some of the work done by the lift is transferred to the skier in the form of mechanical energy, and the whole process starts again. Some of the work done by the chairlift, however, is lost. Understanding how to measure work and compare it to potential energy gains in the presence and absence of friction will help you understand this process.
Graphical Representation of Work
What is work? When an object, such as a skier, is lifted at a constant velocity, work is being done against the force of gravity. Recall the earlier definition of work from Module 6: Lesson 1.
Work is a measure of the amount of energy transferred when a force acts over a given displacement. It is the product of the magnitude of the applied force and the displacement of the object in the direction of that force. Expressed as an equation, it is
This is often written as 
| Quantity | Symbol | SI Unit |
| work | W | joule (J or N•m) |
| force (the component of the force that is parallel to the displacement of the object) | F|| | newton (N) |
| displacement (in the same direction as force) | d | metre (m) |
1 J is equal to 1 N•m. Work is the product of the magnitudes of two vector quantities. Hence, it is a scalar quantity.
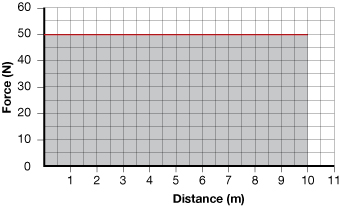
The equation is easily represented graphically as the area under a force-distance graph because the area is equal to the product of force and distance. For example, if a 50.0-N force acts through a distance of 10.0 m, how much work is done by the force?
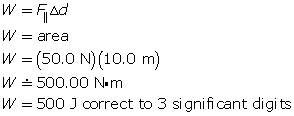
Understanding the Component of Force That Does the Work
In the equation W = F||Δd, F|| represents the component of the force that acts in the same direction as the motion (it is parallel to the motion) and Δd represents the change in position. In many cases, however, the force and displacement are not in the same direction.
Recall that component analysis is used to find the work done when the force is not in the same direction as the displacement.
In these situations, the work equation becomes W = F cos(θ)Δd, where θ is the angle between the direction of the force and the direction of the change in position (Δd).
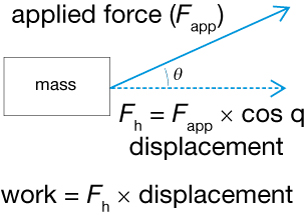
If the angle between F and Δd is not constant, it will be necessary to recalculate W = F cos(θ)Δd for each value of θ and Δd and then add the results. When you do this, you still find that the area under a force-displacement graph equals the work done by that force.
Now you will use this fact to investigate the relationship between the work done and the gain in mechanical energy when an object is lifted in the presence of conservative forces (gravity) and non-conservative forces (friction).