Module 4—Gravitational Force
Explore
Henry Cavendish used a torsion balance in his experiments.
Earth was weighed in 1798 by Henry Cavendish. In doing so, he experimentally verified Newton’s law of universal gravitation. Until this had been done, the exact mathematical relationship between the force of gravity and the mass causing it was unknown.
What was known was that the force of gravity varied with the product of the masses and varied inversely to the square of the distances separating them. Describing this mathematically produces the following proportionality:
In order to make this an equation, a proportionality constant is introduced. In this case, the constant is the universal gravitational constant (G). As you saw in the last lesson, it is related to the force of attraction between two masses and the distance separating them, as follows:
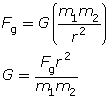
The Cavendish Experiment
Based on this relationship, Cavendish set out to measure the force of attraction between two large metal balls of known mass separated by a known distance. It was clear that the force of attraction would be very small. (Remember, the force of attraction between two masses is not significant until the masses are extremely large.) A torsion balance was used to accurately measure the small forces that were expected. A torsion balance is a device that measures the amount of “twisting” that occurs along a suspension fibre or cable. It had been invented 20 years before Cavendish performed his experiment.
By measuring the force of attraction between two large sets of lead balls with a given mass and distance of separation, Cavendish determined that the value of the universal gravitational constant is 
.
Watch and Listen
Watch the Cavendish video to see one method of weighing Earth.
Read
Read about Cavendish’s experiment in “Determining the Value of the Universal Gravitational Constant” on pages 205 and 206 of the physics textbook.
Module 4: Lesson 3 Assignment
Remember to submit the answers to TR 1 and TR 2 to your teacher as part of your Module 4: Lesson 3 Assignment.
Try This
TR 1. Explain how Cavendish was able to determine the force of attraction in his experimental apparatus.
TR 2. The mass of each lead ball in Cavendish’s experiment was 195 kg. Given the value of G, what would be the expected force of attraction between two of these balls if their centres were separated by 1.0400 m?
Measuring the Mass of Earth
© Selahattin Bayram/shutterstock
By determining the value for the universal gravitational constant, Cavendish indirectly measured the mass of Earth based on the following mathematical relationships:
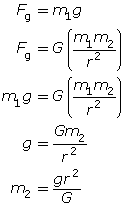
The method Cavendish used is still the method used for finding Earth’s weight accurately. You can read about the results of a recent experiment on the web. Use the following keywords to search for information on the Internet: “space,” “physicists,” “forces,” “Earth,” “drop,” and “weight.”
Module 4: Lesson 3 Assignment
Remember to submit the answer to TR 3 to your teacher as part of your Module 4: Lesson 3 Assignment.
Try This
TR 3. Given the value for the universal gravitational constant, the average value for the acceleration due to gravity at the surface of Earth, and the radius of Earth, determine Earth’s mass. (Earth’s radius can be found on the physics data sheet in the Constants section along with other useful information.)
Constants
Acceleration Due to Gravity Near Earth 
Gravitaional Constant G = 6.67 × 10-11 N•m2/kg2
Radius of Earth re = 6.37 × 106 m
Mass of Earth Me = 5.98 × 1024 kg
Elementary Charge e = 1.60 × 10-19 C
Coulomb's Law Constant k = 8.99 × 109 N•m2/C2
Electron Volt 1eV = 1.60 × 10-19 J
Index of Refraction of Air n = 1.00
Speed of Light in Vacuum c = 3.00 × 108 m/s
Planck's Constant h = 6.63 × 10-34 J.s
h = 4.14 × 10-15 eV.s
Atomic Mass Unit u = 1.66 × 10-27 kg
Self-Check
SC 1. Given the mass of the Moon is 7.3477×1022 kg and it has a mean radius of 1737.103 km, determine the value for the acceleration due to gravity on the surface. Explain how this would affect your walking speed.
Self-Check Answers
SC 1.
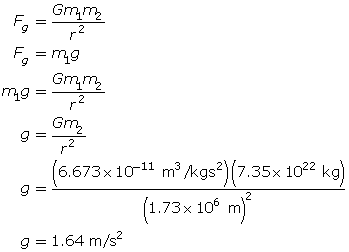
Your walking speed would be increased as your weight would be reduced to 1/6th its value on Earth, which would make motion easy.
Module 4: Lesson 3 Assignment
Remember to submit the answer to TR 4 to your teacher as part of your Module 4: Lesson 3 Assignment.
Try This
TR 4. Density is a measure of the mass per unit of volume for a material. Mathematically, this can be expressed in units of kg/m3. Given that the equation for the volume of sphere is based on radius, determine the density of Earth and compare it to that of water (998 kg/m3 at 20ºC). Explain how this helps people understand Earth’s interior.
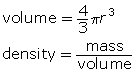
Self-Check
SC 2. Given the mass of Neptune is 1.03 ×1026 kg and that it has an equitorial radius of 2.48 × 107 m, determine the value for the acceleration due to gravity on the equator of Neptune.
Self-Check Answers
SC 2.
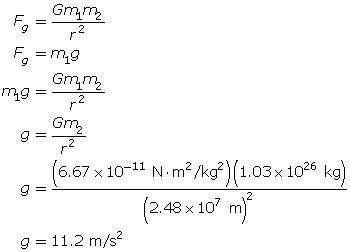
Density is a measure of the mass per unit of volume for a material. Mathematically, this can be expressed in units of kg/m3. Given that the equation for the volume of sphere is based on radius, determine the density of Earth and compare it to that of water (998 kg/m3 at 20ºC). Explain how this helps people understand Earth’s interior.
Self-Check
SC 3. Complete question 2 of “Practice Problems” on page 207 of the physics textbook.
Self-Check Answers
SC 3.
Given
mT = 4.6 × 107 kg
Fg = 61 N
r = 100 m
Required
the mass of the iceberg (mi)
Analysis and Solution
Assume that the distance is between the centres of the Titanic and the iceberg. Use Newton’s law of universal gravitation and rearrange the equation to solve for mass.
Paraphrase
The mass of the iceberg was 2.0 × 108 kg.