Module 1—Motion
Method 4: Cartesian Method (x and y Components)
The fourth way to define a vector direction is fundamentally different than the three methods you have explored so far. In each of the previous methods, the magnitude and direction of the vector are described by two separate bits of information—one value for the magnitude and another for the direction (in one of three possible specifications). The fourth method uses x and y components on a Cartesian system to describe both the magnitude and direction of a vector.
 Watch and Listen
Watch and Listen
Watch an animation to see how the direction of a vector can be indicated in different ways. The Cartesian Vector Components simulation will summarize previously studied methods and introduce the Cartesian method (x and y components) of vector specification.
 Try This
Try This
You can learn more about the how x and y components are just another version of the navigator method and the Cartesian method using the Vector Specification computer simulation previously encountered. Note that the simulation uses slightly different terminology, and this application further subdivides the Cartesian method into three additional categories. However, the simulation is a great way to explore the use of angles to describe vector directions.
Re-open the Vector Specification simulation.
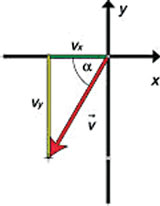
Figure 4
TR 9. On the control panel of the simulation, select the “Polar (positive)” mode in the control panel of the simulation, and enter 150 for the magnitude and 240 for the angle. Then select the “Cartesian (vx, vy)” mode on the control panel. Verify that the display matches Figure 4, except for the numbers at the tip of the vector, which will not be present in the display.
The projections of the vector onto the x- and y-axes, shown in green and yellow, respectively, are called the scalar components of the vector. They are called scalar components because they are numbers. The scalar components are equal to the x and y coordinates of the tip of the vector if the tail end of the vector is at the origin of the coordinate system, as it is here. The coordinates have been added to the display in Figure 4.
The x and y scalar components of a vector,![]() , are denoted vx and vy, respectively. In the present case, this pair of components has the value (vx, vy) = (–75.00, –129.90).
, are denoted vx and vy, respectively. In the present case, this pair of components has the value (vx, vy) = (–75.00, –129.90).
You can use the notation (vx, vy) to denote the vector ![]() , because the vector is fully specified in terms of its two scalar components. Thus, when required to calculate a vector,
, because the vector is fully specified in terms of its two scalar components. Thus, when required to calculate a vector,![]() , you can give the final answer in the form above. There is no need to calculate the magnitude and direction of the vector because the components contain this information.
, you can give the final answer in the form above. There is no need to calculate the magnitude and direction of the vector because the components contain this information.
You could state your final answer in the form,![]() .
.
However, when describing a vector by its two components, it must be understood from the context how the x- and y-axes are defined. In this case, the axes are defined as number lines with positive and negative directions.
Example 1
Given the magnitude and direction of a vector, how are the components (vx, vy) calculated?
First, make a diagram showing the relevant quantities, as shown in Figure 5.

Figure 5
The diagram shows a right-angle triangle containing the vector, ![]() , as the hypotenuse, with the other two sides equal to vx and vy, or rather, equal to their magnitudes |vx| and |vy| (since vx and vy are both negative in the present case). The angle, represented here by the Greek letter alpha (α), defines the orientation of
, as the hypotenuse, with the other two sides equal to vx and vy, or rather, equal to their magnitudes |vx| and |vy| (since vx and vy are both negative in the present case). The angle, represented here by the Greek letter alpha (α), defines the orientation of ![]() . In order to apply trigonometric functions to solve for the components, you need to know this angle.
. In order to apply trigonometric functions to solve for the components, you need to know this angle.
TR 10. Find this angle using the simulation. On the control panel of the simulation, select the “Polar (positive)” mode, and enter 150.00 for the magnitude and 240.00 for the angle. Then select the “Navigational” mode and “S of W” from the drop-down menu on the control panel.
α = _________
Knowing angle α allows you to use basic trigonometry to solve for the vertical component, vy.
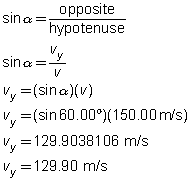
Figure 5 shows that vy is downward and, therefore, negative.
vy = –129.90 m/s
Basic trigonometry is also used to solve for the horizontal component, vx:
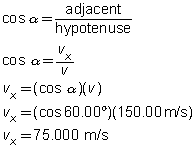
Figure 5 shows that vx is directed towards the left and is, therefore, negative.
vx = –75.000 m/s
The vector components are correctly written as (–75.000 m/s, –129.90 m/s).
Again, remember units are normally always included in calculations. Units are not shown here because the simulation cannot accommodate them.
Example 2
Given scalar components vx and vy, how are the magnitude and direction of a vector,![]() , calculated?
, calculated?
Applying the Pythagorean theorem (c2 = a2 + b2) to the right-angle triangle in Figure 5 gives v = 150.0.
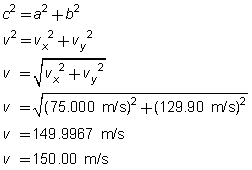
Applying the definition of the tangent to the right-angle triangle in Figure 5 gives α = 60.00º.

Combining the magnitude and angle gives the value of the vector:
![]() = 150.00 m/s [60.0° S of W]
= 150.00 m/s [60.0° S of W]
or
![]() = 150.0 m/s [30.0° W of S]
= 150.0 m/s [30.0° W of S]
Simulation Summary
While working with the simulation, you found that the direction of a vector can be specified in a number of different ways. You can use
-
the Cartesian method:
-
positive angles measured from the positive x-axis in a counterclockwise direction—for example, 32.1 m/s [327°]
-
negative angles measured from the positive x-axis in a clockwise direction—for example, 27.8 m/s [–123°]
-
direction implicitly contained in the x and y components
-
-
the navigator method:
-
measure direction with compass bearings—for example, 1.7 m/s [38° E of N]
-
 Read
Read
To learn more about determining vector components, read pages 83 to 84 of your textbook. Pay special attention to the use of units, particularly in “Example Problem 2.4” on page 84.
 Self-Check
Self-Check
SC 4. The vector, ![]() , has the following components: vx = –75.0 m/s, vy = +200 m/s. Calculate the magnitude and polar positive direction of the vector,
, has the following components: vx = –75.0 m/s, vy = +200 m/s. Calculate the magnitude and polar positive direction of the vector,![]() . Show your work, and check your solution by setting it up in the simulation.
. Show your work, and check your solution by setting it up in the simulation.
SC 5. Given the vector 126 m/s [65.0° N of E], calculate the x and y components. Show your work, and check your solution by setting it up in the simulation.
 Self-Check Answers
Self-Check Answers
SC 4.
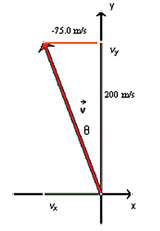
vx = –75.0 m/s, vy = +200 m/s
Required
the magnitude and polar positive direction of the vector, ![]()
Analysis and Solution
Use the theorem of Pythagoras to calculate the magnitude of the vector and the tangent function to calculate the direction. The fact that the x component is negative and the y component is positive indicates that the vector will be in the second quadrant. Therefore, add 90° to the angle found by calculation to give the polar positive angle.
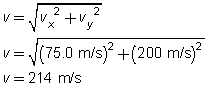
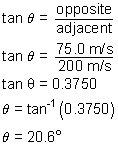
The polar positive angle is found by: 90.0° + 20.6° = 110.6°
Paraphrase
The magnitude and polar positive direction of the vector, ![]() , is 214 m/s [110.6°].
, is 214 m/s [110.6°].
SC 5.
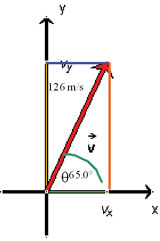
Given
The vector is 126 m/s [65.0° N of E].
Required
to find the x and y components (vx) and (vy)
Analysis and Solution
Use the cos function to find the vx and the sin function to find the vy.


Paraphrase
The x and y components are 53.2 m/s and 114 m/s, respectively.
 Module 1: Lesson 1 Assignment
Module 1: Lesson 1 Assignment
Remember to submit the answers to TR 11 and TR 12 to your teacher as part of your Module 1: Lesson 1 Assignment.
 Try This
Try This
TR 11. The vector,![]() , has the following components: vx = +65.0 m/s, vy = –120 m/s
, has the following components: vx = +65.0 m/s, vy = –120 m/s
Calculate the magnitude and polar positive direction of the vector,![]() . Show your work, and check your solution by setting it up in the simulation.
. Show your work, and check your solution by setting it up in the simulation.
TR 12. Given the vector 225 m/s [35.0°W of S], calculate the x and y components. Show your work, and check your solution by setting it up in the simulation.
 Module 1: Lesson 1 Assignment
Module 1: Lesson 1 Assignment
Remember to submit the answers to TR 13, TR 14, TR 15, and TR 16 to your teacher as part of your Module 1: Lesson 1 Assignment.