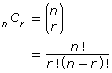Module 8 Summary

 

In this module you looked at different ways people are identified through arrangements of numbers or the arrangements of numbers and letters. There are many ways you are identified, like your PIN when using a bank machine, your passport number, or your phone number. In the module you learned how to determine the total possible arrangements of numbers to make up these identification numbers.

 

This is a collage of three photos, including a person entering a PIN code at a bank machine, a Canadian passport, and a phone number being dialed.

passport: photodisc/Thinkstock; bank machine: iStockphoto/Thinkstock; remote: iStockphoto/Thinkstock; Canadian Passport Cover (Ottawa: Passport Canada, 2011). Reproduced with permission.

 

In this module you investigated the following questions:

You learned how to use tree diagrams, outcome charts, and the fundamental counting principle to determine the total number of outcomes. You also learned how to use factorial notation as a new notation.

 

You learned how to determine the number of permutations using the fundamental counting principle and nPr. You also determined the possible outcomes when there are repetitions or other restrictions.

 

You learned how to use combinations to solve counting problems where the order is not important.

 

You learned how to expand a binomial using the binomial theorem instead of multiplying out all the factors.

 

In Module 8 Project: Creating the Ultimate Password, you investigated ways of creating passwords to reduce the chance of identity theft.

 

Some of the key ideas from each lesson are shown in the following table.

 

Lesson 1

The fundamental counting principle can be used to determine the number of possible arrangements of items. If one task can be performed in a ways, a second task in b ways, and a third task in c ways, the number of ways to calculate the possible arrangements of all three tasks is a × b × c.

 

Factorial notation can be used as an abbreviation for products of successive integers.
when n is a natural number.

Lesson 2

Permutations are used when the order of the objects is important.

 

 

nPr, where 0 ≤ r ≤ n

 

 

 

The number of permutations of n objects when a objects are identical, b objects are identical, c objects are identical, and so on is

 

 

Lesson 3

Combinations are used when the order of the objects is not important. The following formula can be used to calculate a combination where 0 ≤ n ≤ r 

 

 

Lesson 4

The binomial theorem is used to expand a binomial using a pattern that involves combinations. The generalized binomial theorem is

 

 

Any term of the expansion can be determined using the following formula:

 

 

tk + 1 = nCk (x)n − k (y)k

 

The Mathematics Programs of Studies Page on the LearnAlberta website may be helpful for a review of this module.

 

On the left side under “Outcomes,” click on “30-1,” then click on “Permutations, Combinations & Binomial Theorem (30-1).”

 

Look at Specific Outcomes 1 to 4. Click on the image that follows each outcome (This image represents the student resources.) to take you to a list of student resources. Choose the resources you would like to access to review Module 8.