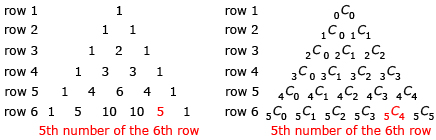
The value of an entry in Pascal’s triangle can be determined using combinations. nCk is equal to the value of the (k + 1)th number of the (n + 1)th row. For example, in 5C4, k = 4 and n = 5. So, you need to look to the (4 + 1)th, or 5th, number in the (5 + 1)th, or 6th, row. So, 5C4 = 5.

 

 

So far you have seen a pattern for determining

• the exponents of a binomial expansion
• a method for determining the coefficients of a binomial expansion using Pascal’s triangle
• a method of determining the values of Pascal’s triangle using combinations

Putting these together results in the binomial theorem, which can be used to determine each term of a binomial expansion. You may have already determined your own version of the binomial theorem in Try This 3. One common way of writing the theorem is as follows:

 

(x + y)n = nC0(x)n(y)0 + nC1(x)n−1(y)1 + nC2(x)n−2(y)2 ++ nCn−1(x)1(y)n−1 + nCn(x)0(y)n

 

Try to match the terms of this expression to the expression you began to expand in Try This 3.

 

 

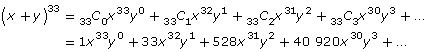
If you are interested in a particular term, the following formula can be used:

 

tk+1 = nCk(x)n−k(y)k

 

Watch Term of a Binomial Expansion to see how this formula is used to determine the sixth term of (3f − g2)14.

 

---