Module 8: Lesson 4
Self-Check 1
-
- The next row is
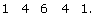
- The next row is
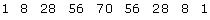 .
.
- The next row is
-
- There are five terms.
- There are eight terms.
- There are q + 1 terms.
-
- The question has been solved by using the series of patterns, as was determined earlier:
- In the expansion of the binomial (a + b)9, the values of the numerical coefficients are equivalent to the 10th row in Pascal’s triangle. Following the pattern of Pascal’s triangle, the 10th row looks as follows, with the 6th term highlighted:
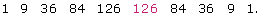
- In the expansion of the binomial (a + b)9, the variable in the first term will start at a9, and will decrease by 1 until arriving at the 6th term. Thus, the 6th term will be a4.
- Because the degree of each term must be equal to 9, the exponent on the b variable will be 5. Thus, literal coefficients in the 6th term will be a4b5.
- The 6th term in the expansion of the binomial (a + b)9 is 126a4b5
- In the expansion of the binomial (a + b)9, the values of the numerical coefficients are equivalent to the 10th row in Pascal’s triangle. Following the pattern of Pascal’s triangle, the 10th row looks as follows, with the 6th term highlighted:
- This question will be solved in the same way that 7.a. was solved, but with some additional complexities added:
- In the expansion of the binomial (x − 3y)6, the values of the numerical coefficients are equivalent to the 7th row in Pascal’s triangle. Following the pattern of Pascal’s triangle, the 7th row looks as follows, with the 4th term highlighted:
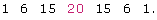
- In the expansion of the binomial (x − 3y)6, the variable in the first term will start at x6, and will decrease by 1 until arriving at the 4th term. Thus, the 4th term will be x3.
- Because the degree of each term must be equal to 6, the exponent on the second term in the binomial will be 3. In this case, however, the second term is not just a positive value with a single variable. The second term is −3y. In order to solve for this component, the entire term must be used as the base. This is then taken to the power of 3: (−3y)3.
- The 4th term in the expansion of the binomial (x − 3y)6 is 20x3(−3y)3. This can be further simplified in the following way:
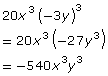
- Thus, the 4th term in the expansion of the binomial (x − 3y)6 is −540x3y3.
- In the expansion of the binomial (x − 3y)6, the values of the numerical coefficients are equivalent to the 7th row in Pascal’s triangle. Following the pattern of Pascal’s triangle, the 7th row looks as follows, with the 4th term highlighted:
- The question has been solved by using the series of patterns, as was determined earlier:
-
- There are 13 terms.
- This question will be solved in the same way that 7.a. was solved.
- In the expansion of the binomial (x + y)12, the values of the numerical coefficients are equivalent to the 13th row in Pascal’s triangle. Following the pattern of Pascal’s triangle, the 13th row looks as follows, with the 4th term highlighted:
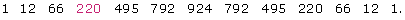
- In the expansion of the binomial (x + y)12, the variable in the first term will start at x12 and will decrease by 1 until arriving at the 4th term. Thus, the 4th term will be x9.
- Because the degree of each term must be equal to 12, the exponent on the y variable will be 3. Thus, literal coefficients in the 4th term will be x9y3.
- The 4th term in the expansion of the binomial (x + y)12 is 220x9y3.
- In the expansion of the binomial (x + y)12, the values of the numerical coefficients are equivalent to the 13th row in Pascal’s triangle. Following the pattern of Pascal’s triangle, the 13th row looks as follows, with the 4th term highlighted:
-
- This question will be solved in the same way that 7.a. was solved.
- In the expansion of the binomial (x + y)3, the values of the numerical coefficients are equivalent to the 4th row in Pascal’s triangle. Following the pattern of Pascal’s triangle, the 4th row looks as follows:
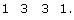
- In the expansion of the binomial (x + y)3, the variables in the first term will start at x3y0, the exponent on x will decrease by 1, and the exponent on y will increase by 1.
- In the expansion of the binomial (x − y)3, the coefficients will change because −1 is multiplied by the y variable, so each odd exponent on the y variable will result in a negative coefficient.
- The expansion of (x + y)3 is 1x3 + 3x2y + 3xy2 + 1y3.
- The expansion of (x − y)3 is 1x3 − 3x2y + 3xy2 − 1y3.
- The expansions are different because the signs for the 2nd and the 4th terms are positive in the expansion of (x + y)3 and are negative in the expansion of (x − y)3.
- In the expansion of the binomial (x + y)3, the values of the numerical coefficients are equivalent to the 4th row in Pascal’s triangle. Following the pattern of Pascal’s triangle, the 4th row looks as follows:
- The equation (x + y)3 + (x − y)3 = 2x(x2 + 3y2) can be shown to be equivalent by manipulating the left side until it equals the right side.
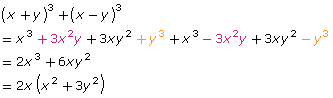
The left side is equal to the right side, so the equation is correct. - The solution for (x + y)3 − (x − y)3 can be found as follows:
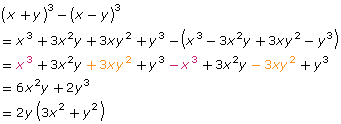
The expansion of (x + y)3 − (x − y)3 looks similar to the expansion of (x + y)3 + (x − y)3, except that, when simplified, the coefficients for the x2- and y2-values inside the bracket are reversed. Similarly, the factor that is taken out of the expression uses different variables.
- This question will be solved in the same way that 7.a. was solved.
© 2012 Alberta Education