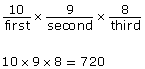Explore

 

In Discover you saw different ways of calculating the number of permutations. The “Permutations” applet used lists, tree diagrams, and the fundamental counting principle. You also calculated the number of arrangements when you used all or some of the tiles.

 

In Lesson 1 you saw another way to calculate the number of permutations by drawing blanks to represent the problem.

 

In how many ways can horses finish first, second, and third if there are 10 horses in a race?

 

	You can draw blanks to represent finishing first, second, and third.
	Assuming every horse is equally likely to win, you know the first position can be filled in ten ways.
	The second-place finisher could be any of the nine remaining horses.
	The third-place finisher could be any of the remaining eight horses.
	Applying the fundamental counting principle, the number of ways the first-, second-, and third-place positions could be filled is 10 × 9 × 8, or 720 different ways.

 

Notice that the order of the finish is important. If three horses finish in the order A, B, and C, that order is a different result from a finish of C, B, and A, even though the arrangement contains all the same horses.
 

Try This 2

 

You know that if you’re trying to find the number of ways all ten horses could finish, it would be 10! = 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1. Because you are only interested in the first three places, there is only 10 x 9 x 8. Is there a way to represent this information in factorial notation?

1. Why are only three terms, 10 × 9 × 8, used to find the solution?
2. 10 × 9 × 8 is no longer multiplied by the remaining factors, 7 × 6 × 5 × 4 × 3 × 2 × 1. What mathematical operation has to be performed on 7 × 6 × 5 × 4 × 3 × 2 × 1 so that the new product becomes 1?
3. Write 7 × 6 × 5 × 4 × 3 × 2 × 1 in factorial notation.
4. Write 10 × 9 × 8 as a quotient using factorial notation.
5. Determine an expression for the denominator that uses the total number of horses, 10, and the number 3, which represents finding those that finished first, second, and third.

Save your responses in your course folder.

 

Share 1

 

With a partner or group, share your solutions to questions 4 and 5. How do your quotients compare?

 

Based on your solution to question 5 in Try This 2, find a general expression for the number of permutations of n objects arranged r at a time.

 

If required, save a record of this information in your course folder.