Module 7 Summary

 

A collage demonstrating various forms of transportation.

Hemera/Thinkstock

 

In this module you investigated the following questions:

In the first half of this module you explored rational functions, mainly graphically. You determined when both asymptotes and points of discontinuity occurred. You also approximated the solutions to rational equations graphically. The second half of this module focused on function operations. You added, subtracted, multiplied, divided, and composed functions. You also used these operations to solve some problems. In the Module 7 Project: Shipping Wars, you applied an understanding of rational functions and function operations to a transportation business and used these understandings to determine functions that represented various relationships.

 

Following are some of the key ideas that you learned in each lesson.

 

Lesson 1

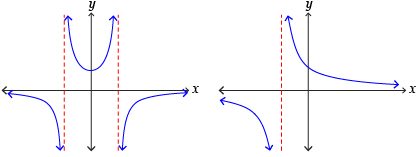
Rational functions can be graphed and transformed in a manner similar to other functions. Many rational functions include asymptotes.

 

This diagram shows two rational functions and their asymptotes.

Lesson 2

Asymptotes and points of discontinuity are two types of discontinuities that occur at non-permissible values for rational functions.

 

This diagram shows a point of discontinuity and states “Points of discontinuity or ‘holes’ occur when a factor in both the numerator and denominator equals 0.” The diagram also shows an asymptote and states “Vertical asymptotes occur when a factor only in the denominator equals 0.” The diagram also shows an x-intercept and states “x-intercepts occur when a factor only in the numerator is equal to 0.”

Lesson 3

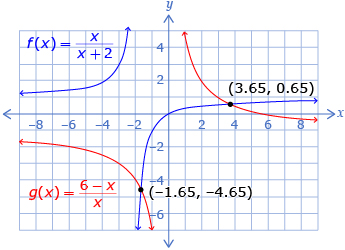
The graphs of rational functions can be used to approximate the solutions to rational equations.

 

This diagram shows function f at x equals x divided by all of x plus 2, and function g at x equals all of 6 minus x, divided by x. The intersections of the two functions at points (3 decimal 65, 0 decimal 65) and (negative 1 decimal 65, negative 4 decimal 65) are shown.

Lesson 4

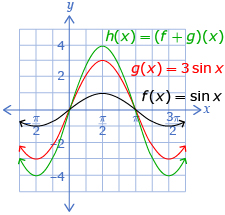
Two functions can be added or subtracted. The notations (f + g)(x) and (f − g)(x) are often used to represent f(x) + g(x) and f(x) − g(x).

 

This diagram shows three functions. One function is of f at x equals the sine of x. The second function is of g at x equals 3 times the sine of x. The third function is of h at x equals f at x plus g at x. The third function has roots at 0 radians, pi radians, and 2 pi radians (and every pi radians after that). For the domain between 0 and 2 pi, it has a maximum that occurs at (pi divided by 2, 4) and a minimum that occurs at (negative 3 pi divided by 2, negative 4).

Source: Pre-Calculus 12. Whitby, ON: McGraw-Hill Ryerson, 2011. Reproduced with permission.

 

 

Lesson 5

Two functions can be multiplied or divided. The notation (f + g)(x) and can be used to represent f(x) × g(x) and .

Lesson 6

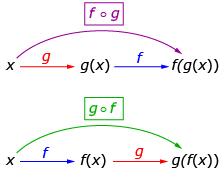
The output from one function can be used as the input for another function by using a composition of functions. The notation (f o g)(x) is often used to represent f(g(x)).

 

The first diagram shows that f composed with g can be described by applying function g to x to give g at x and then applying function f to g at x to give f at g at x. The second diagram shows that g composed with f can be described by applying function f to x to give f at x and then applying function g to f at x to give g at f at x.