Module 6 Summary

 

This is a photo of bacteria in Petri dishes.

Valueline/Thinkstock

In this module you used exponential and logarithmic functions to describe the relationship between time and the growth or decay of different quantities. As examples, you looked at the growth of money and bacteria, the decay of radioactive isotopes, and the use of the pH scale to describe the change in the concentration of hydrogen ions in solutions.

 

You investigated the following question:

This is a photo of a solution and a pH strip.

iStockphoto/Thinkstock

You learned how to graph exponential and logarithmic functions and how transformations can be applied to these functions. You also learned that a logarithm is the inverse of an exponential function. You can convert between exponential and logarithmic form and vice versa. You explored different logarithmic scales, such as the Richter scale, the pH scale, and the decibel scale. Lastly, you studied a variety of methods that could be used to solve exponential and logarithmic equations.

 

In the Module 6 Project on box-office movie revenues, you explored how the cumulative revenue of movies could be described as exponential and logarithmic functions. You also determined decibel levels of movies using the logarithmic decibel scale. Finally, you solved an exponential equation involving movie revenues.

 

Here are some of the key ideas you learned in each lesson.

 

Lesson 1

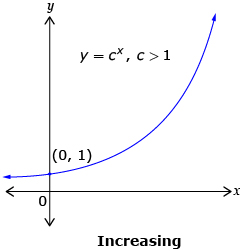
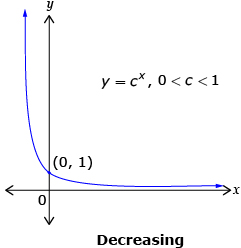
The characteristics of all exponential functions of the form y = cx, c > 0, c ≠ 1 are as follows.

  • If c > 1 then the function is increasing and is an exponential growth function.

     
    This is a graph of a curve y equals c to the exponent x with c value greater than one. The curve increases with the point (0, 1) indicated.

    Source: Pre-Calculus 12. Whitby, ON: McGraw-Hill Ryerson, 2011.
    Reproduced with permission.



  • If 0 < c < 1 then the function is decreasing and is an exponential decay function.

     
    This is a graph of a curve y equals c to the exponent x with c value greater than zero and less than one. The curve decreases with the point (0, 1) indicated.

    Source: Pre-Calculus 12. Whitby, ON: McGraw-Hill Ryerson, 2011.
    Reproduced with permission.



  • The domain is {x|x ∈ R}.
  • The range is {y|y > 0, y ∈ R}.
  • There is no x-intercept.
  • The y-intercept is 1.
  • The horizontal asymptote is at y = 0.

Transformations of exponential functions are similar to transformations of other functions, as seen in Module 1.

Lesson 2

Follow these steps to solve exponential equations where the bases can be written as powers with the same base:

  • Use the laws of exponents to write each side of the equation as powers with the same base.
  • Use the property if bx = by, then x = y, where b ≠ −1, 0, 1.
  • Solve for the variable.

Take this approach to solve exponential equations where the bases cannot be written as powers with the same base:

  • Use an educated guess-and-check method to estimate an answer.

Lesson 3

A logarithmic function is the inverse of an exponential function. Use this approach to convert an exponential form to a logarithmic form:

The logarithmic function is the reflection of the exponential function in the line y = x. The characteristics of the logarithmic function y = logc x, c > 0, c ≠ 1 are as follows:

  • The domain is {x|x > 0, x ∈ R}.
  • The range is {y|y ∈ R}.
  • The x-intercept is 1.
  • The vertical asymptote is x = 0, or the y-axis.

Lesson 4

In a logarithmic function of the form the parameters a, b, h, and k correspond to the following transformations:

 

Parameter

Value > 0

Value < 0

a
  • vertical stretch of graph by a factor of |a|
  • vertical stretch of graph by a factor of |a| and a reflection in the x-axis

b
  • horizontal stretch of graph by a factor of
  • horizontal stretch of graph by a factor of  and a reflection in the y-axis

h
  • translated to the right h units
  • translated to the left |h| units

k
  • translated up k units
  • translated down |k| units

Lesson 5

The following laws of logarithms were studied:

  • product law of logarithms

     
    logb (M × N) = logb M + logb N 
  • quotient law of logarithms

     

  • power law of logarithms

     
    logb (Mn) = nlogb M

Lesson 6

To solve logarithmic equations you can use the property if logc A = logc B, then A = B, where c, A, B > 0 and c ≠ 1.

 

To solve exponential equations you can use the property if A = B, then logc A = logc B, where c, A, B > 0 and c ≠ 1.