Module 5: Lesson 3
Self-Check 3
- Questions 4.c., 7, 11, 13, and 14 on pages 296 to 298 of the textbook
-
- To solve this question, it will be necessary to make use of the Pythagroean theroem identities that were just discussed.
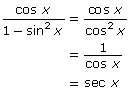
- To solve this question, it will be necessary to make use of the Pythagroean theroem identities that were just discussed.
-
- By using the Pythagorean theorem identity sin2 θ + cos2 θ = 1 and rearranging it, the expression 1−sin2 θ becomes cos2 θ.
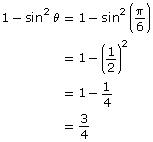
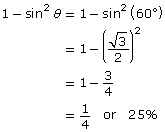
-
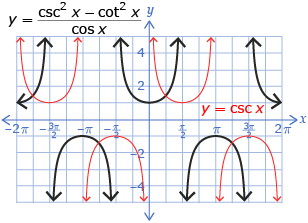
- The graphs of
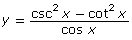 and y = csc x are shown.
and y = csc x are shown.
The graphs of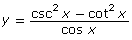 and y = sec x are shown.
and y = sec x are shown.
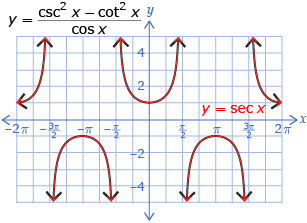
Based on the graphs, it appears as though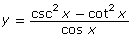 is equivalent to y = sec x.
is equivalent to y = sec x. - For the equation
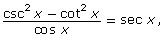 the non-permissible values will occur when either csc2 x, cot2 x, or sec x is undefined. It will also occur when cos x = 0.
the non-permissible values will occur when either csc2 x, cot2 x, or sec x is undefined. It will also occur when cos x = 0.
cos x = 0 at
csc2 x is undefined at {x = nπ, n ∈ I, x ∈ R}.
cot2 x is undefined at {x = nπ, n ∈ I, x ∈ R}.
sec x is undefined at
When the two sets of restrictions are put together, the resulting set of restrictions is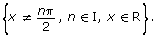
- While there is more than one way to rearrange
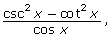 only one method is shown.
only one method is shown.
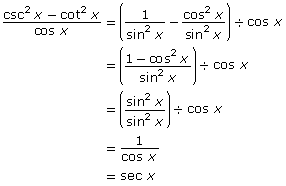
- The graphs of
-
- After Stan’s substitution, the following answer is obtained:
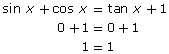
- After Lina’s substitution, the following answer is obtained:
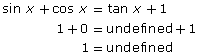
The left side of the equation is equal to 1, but the right side of the equation is undefined. - Lina’s substitution gives an undefined solution for tan x. Because one of the terms is undefined, this is a non-permissible value.
- After Giselle’s substitution, the following answer is obtained:
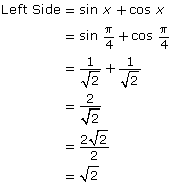
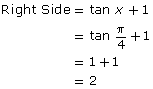
She discovers that the two answers are not equivalent.
- The three students have enough information to determine that the equation given is not an identity. Once Giselle identified a permissible value for which the equation was not true, they could safely conclude that the equation was not an identity.
- After Stan’s substitution, the following answer is obtained:
- While there are multiple ways in which this expression can be simplified, only one method is shown.
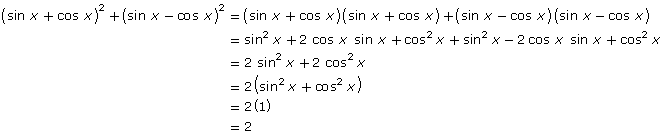
-
© 2012 Alberta Education