Module 4 Summary

 

This is a photo of a Ferris wheel at night.

iStockphoto/Thinkstock

A Ferris wheel moves in a circular motion. This motion is repeated over and over. Being able to describe the location of a person, the distance travelled by a person, or the angle the person has rotated through on the Ferris wheel can be done using trigonometry.

 

In this module you investigated the following question:

You learned there are different ways to express angles, specifically degrees and radians, and you explored the relationship between degrees and radians. You learned about angles in standard position, and you expressed the angles in both degrees and radians. You derived the equation of the unit circle. You applied the equation to describe trigonometric ratios for angles expressed in both degrees and radians.

 

You learned there are three reciprocal trigonometric ratios that can be used in trigonometry, and you determined the value of these trigonometric ratios. You used reference triangles and the unit circle to determine the exact values for the six trigonometric ratios.

 

You solved problems using the six different trigonometric ratios for angles expressed in radians and degrees by using reference triangles and the unit circle. You algebraically solved trigonometric equations of first and second degree, expressed the answers in degrees or radians, and learned there are general solutions to these equations.

 

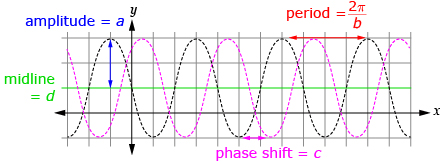
You graphed and analyzed the sine function and the cosine function. You looked at the functions in the form and You saw how changing the values of a, b, c, and d will affect the graphs.

 

In the Module 4 Project you applied what you learned to a Ferris wheel. You examined angles expressed as radians, coterminal angles, and arc length around the Ferris wheel. You discovered how a Ferris wheel can model a unit circle, and you determined how you can use this model to figure out angles and trigonometric ratios. You solved equations related to the Ferris wheel and you looked at the graph of the wheel’s height.

 

Following are some of the key ideas learned in each lesson.

 

Lesson 1

degrees and radians

180° = π radians
Lesson 2

Coterminal angles: the infinite number of angles that are coterminal can be expressed by θ + (360°) n, n ∈ I, or by θ + 2πn, n ∈ I.

 

The arc length formula is a = θr.
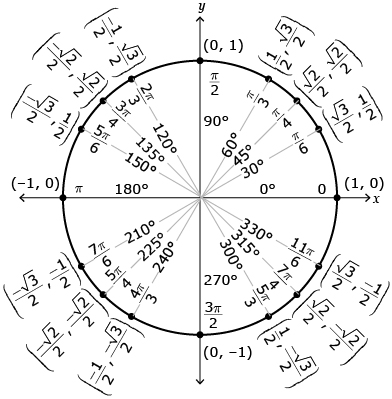
Lesson 3

The equation of the unit circle you derived is x2 + y2 = 1.

 

The Unit Circle

This illustration shows a unit circle cut into 8ths and 12ths. The angles are labelled. The coordinates (0.0) are labeled and the other 15 sets of coordinates are filled in.
Lesson 4

On the unit circle, P(θ) = (cos θ, sin θ). These are six trigonometric ratios:


 
Lesson 5

General solution: the domain for θ is real numbers.


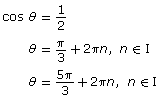To determine the general solution for an equation, find the solutions in one positive rotation and then use the idea of coterminal angles to write the expression.


Example

 

 
Lesson 6 and Lesson 7

Sine and cosine functions: and

 

Parameter

Characteristic of Graph

a

a = amplitude

b

c

c = phase shift right if c is positive, left if c is negative

d

d = midline value

 

Here the amplitude, period, midline, and phase shift are labelled on a sinusoidal graph. The graph also shows that the amplitude equals a, the period equals 2 pi over b, the midline equals d, and the phase shift equals c.

 

The following site may be helpful to use for a review of this module.

 

 
This is a play button that opens Programs of Study.

 

On the left side under “Outcomes,” click on “30-1,” then click on “Trigonometry (30-1).”

 

Look at Specific Outcomes 1 to 5. Click on the image that follows each outcome to take you to a list of student resources. Choose which resources you would like to view to help review Module 4.