The Ferris Wheel

 

Project Overview

 

Purpose

 

In this project you will relate and explain the concepts from Module 4 to the structure and movement of a Ferris wheel.

 

Process

 

Towards the end of the lessons, under Project Connection, you may be prompted to complete a part of the Module 4 Project. You can access the entire project from this page at any time.

 

Make sure to save all work from each Project Connection in your course folder. You will submit your entire Module 4 Project to your teacher at the end of Module 4. Check with your teacher about how you should submit your project work before you begin the project.

 

Presentation

 

The most important part of your project presentation is clearly explaining and supporting your reasoning with relevant visuals and calculations. Make sure to show all your work.

 

Carefully check the Module 4 Project Rubric to be sure you are clear about the expectations for the project.

 

You can choose any format you prefer for the final presentation of this project. Some options include a written document, a virtual or real poster, a website, a video, an oral report, or a slideshow presentation.

Project Introduction

 

The Ferris wheel is a favourite ride at many amusement parks. Its design is a rotating upright wheel with seats or gondolas attached at various points along the rim. The seats are designed to be assisted by gravity to remain upright as the Ferris wheel makes a rotation. Ferris wheels come in a variety of sizes, and the largest one, the Singapore Flyer, reaches 42 stories high and takes riders 165 m up into the sky!

 

Part 1

 

In Part 1 of the project, you will relate angle measures, coterminal angles, arc length, and points on the unit circle to the Ferris wheel.

 

Use Ferris Wheel or any image of a Ferris wheel you have found to help you complete the project.

 

 

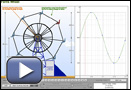
Take a few minutes to play with this animation. Notice that you can change the radius by dragging the seats in and out. You can also change the speed, the direction of rotation, and the number of chairs on the Ferris wheel.

 

Activity 1

1. Choose an angle in standard position within your Ferris wheel.
   1. On a diagram, indicate your starting point and the angle you have chosen expressed in both degrees and radians.
   2. Explain how the angle you chose relates to the direction of rotation of the Ferris wheel.
2. Use the angle from question 1 to help describe the relationship between angle measurements in degrees and radians. Use screen captures and/or images in your explanation.

Save your responses in your course folder. Then return to Lesson 1.

 

Activity 2

 

Choose and record a radius for your Ferris wheel to use in the following questions.

3. Use the angle you chose in Activity 1, and determine two possible coterminal angles. Relate and describe coterminal angles to the movement of someone sitting on the Ferris wheel. Use diagrams to help in your explanation.
4.  
   1. Determine the arc length for the angle you chose in Activity 1. Show your work.
   2. Describe arc length in terms of a person’s experience on the Ferris wheel. Use diagrams to help in your explanation.

Save your responses in your course folder. Then return to Lesson 2.

 

Activity 3

5. Write the equation for the unit circle. If this equation represents the Ferris wheel, what limitations or implications are there on size?
6. Assume the seats are points P(x, y) at the intersection of the terminal arm of an angle and the unit circle. Note: You are working with a model of a Ferris wheel that has a radius of 1.
   1. Indicate on an image of a Ferris wheel the coordinates for one of the seats.
   2. Explain which trigonometric ratio the coordinates of this point would represent.
7. Explain how to determine the exact values of the six trigonometric ratios using the seat coordinates found in question 6.

Save your responses in your course folder. Then return to Lesson 4.

 

Activity 4

 

A beautiful and really large Ferris wheel is among the rides at Edmonton’s Capital EX. The wheel measures about 30 m in diameter, and the bottom of the wheel is about 1 m above the ground. When running at full speed, the Ferris wheel makes a complete rotation in 30 s.

 

An equation to describe the relationship of the height of a seat above the ground and the angle of rotation is h = 15 sin θ + 16, where

• h is the height (in metres) of the Ferris wheel chair above the ground
• θ is the angle the Ferris wheel has rotated through

8. Write an equation to describe the relationship of the height, in metres, of a seat above the ground and the angle of rotation.
   
   h = ___ sin θ + ____
   • In the first blank, enter the radius of the Ferris wheel you chose from the Ferris Wheel applet or from your own image of a Ferris wheel.
   • In the second blank, enter the value of the radius + the height above the ground of the bottom of the Ferris wheel. (The units must be the same.)
9. Choose a height where a seat on your Ferris wheel could be found. Determine the approximate angles θ for 0 < θ < 2π when the height of the Ferris wheel chair is at your chosen height above the ground. Make sure to round your answer to the nearest hundredth of a radian. Use a diagram to describe how the solutions would relate to a person on the Ferris wheel.
10. Explain and show how you can verify your solution is correct.
11. Write the general solution for θ from question 1.
    

Save your responses in your course folder. Then return to Lesson 5.

 

Part 2

 

In Part 2 you will relate sine and cosine graphs and parameters to the Ferris wheel.

 

Open Ferris Wheel, which you used in Part 1.

 

12. In Ferris Wheel, choose dimensions and speed and write your settings in a table like the following.
    
    

    Height to Top (m)	Height to Centre (m)	Loading Platform Height (m)	Radius (m)	Seats	Speed (rev/min)

13. Using Ferris Wheel, make a screen capture of the graph and save the graph in your course folder.

14. Use the graph to complete a table like the following.
    
    

    Amplitude
    Period
    Phase Shift
    Vertical Displacement
    Range
    Domain

15. How do the amplitude, period, and vertical displacement of the graph relate to the properties of the Ferris wheel?

16. Determine the equation of the graph using the information that you recorded in your table in question 14. Explain your reasoning.
17. If you were given a specific time, how would you determine the height of a particular chair on the Ferris wheel? Use an example to explain your answer.

Conclusion

 

Write a brief conclusion to your Module 4 Project. Include a personal reflection of what you feel you learned from the project during and after its completion. Be sure to explain why you feel the way you do.

 

Save your conclusion in your course folder. Then return to Lesson 7.

 

Project Assessment

 

Your Module 4 Project will be evaluated by your teacher using the evaluation guidelines in the project rubric. Read the rubric carefully. Make sure you are aware of how you will be assessed. You can print or save a digital copy of the Module 4 Project Rubric as a guide to help you complete your project.

 

Don’t forget to submit your completed Module 4 Project to your teacher at the end of Module 4.