Module 4: Lesson 5

 

Self-Check 1

 

Questions 10.a., 10.c., and 11.d. on page 202 of the textbook

  1.  

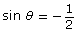    1.  in the domain 0 ≤ θ < 2π

      The ratio sin θ is negative in quadrants 3 and 4. In terms of specific domain, the angle in quadrants 3 and 4 should be included in the solution. The value of the sine ratio is equal to the y-coordinate on the unit circle. The y-coordinate is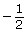 for the angles 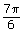and

       

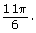
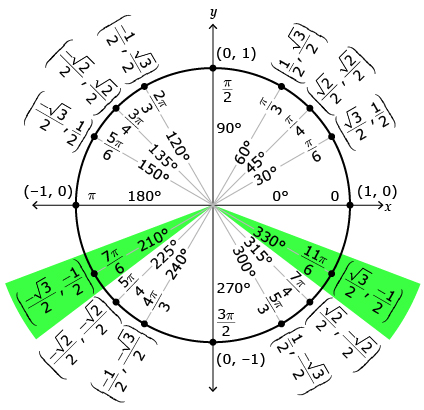
      This is a diagram of the unit circle. The angle seven pi divided by 6 and the coordinates negative square root of 3 divided by 2 are indicated. The angle 11 pi divided by 6 and the coordinates of the negative square root of three divided by 2, and negative 1 divided by 2 are indicated.

      The values are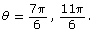



       
      This is a diagram of angles 7 pi divided by 6 and 11 pi divided by 6 in standard position.

      Source: Pre-Calculus 12. Whitby, ON: McGraw-Hill
      Ryerson,       2011. Reproduced with permission.



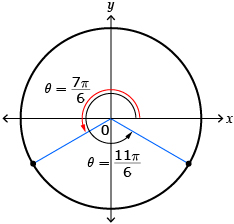
    1. sec θ = 2 in the domain −180° ≤ θ < 90°

      The secant ratio is positive in quadrants 1 and 4, so there should be two values for θ in the specified domain.

       


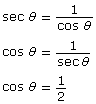
      The value of the cosine ratio is equal to the x-coordinate on the unit circle. The x-coordinate is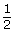 for the angles 60° and 300°.

       

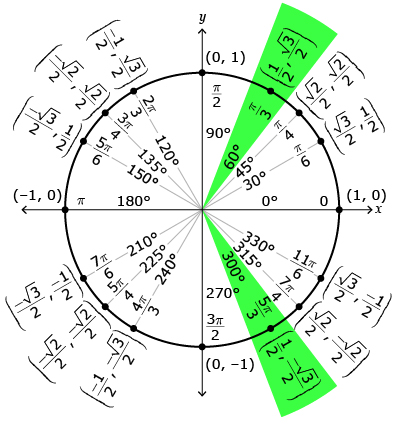
      This is a diagram of the unit circle. Indicated are the angles pi divided by 3 and 5 pi divided by 4 in standard position with the coordinates one-half, along with the square root of 3 divided by 2 and one-half, and the square root of three divided by 2.

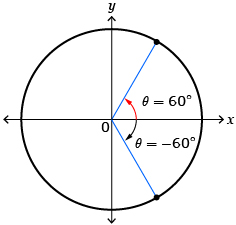
      The 60° is within the specified domain but the 300° is not. There is a negative coterminal angle to 300° in quadrant 4 that would be included in the domain. In quadrant 4,

       



       
      This is a diagram of angles minus 60 degrees and 60 degrees in standard position.

      Source: Pre-Calculus 12. Whitby, ON: McGraw-Hill
      Ryerson, 2011. Reproduced with permission.


  2.  
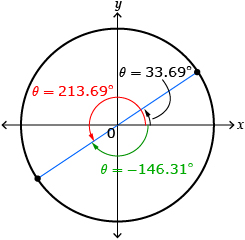
    1. cot θ = 1.5 in the domain −180° ≤ θ < 360°

      The tangent ratio is positive in quadrants 1 and 3. The domain given is −180° ≤ θ < 360°, so there should be three answers.

      To determine the approximate values of θ, you can use your calculator.

      Your calculator should be in degree mode since the specified domain is in degrees.

       


       

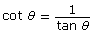
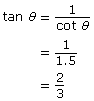
      Use your calculator to determine θ by using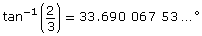

      In quadrant 1,

       
      θ ≈ 33.69°

      In quadrant 3,

       


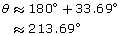
      There would also be this negative angle in quadrant 3.

       


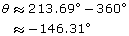
      The values are  θ ≈ −146.31°, 33.69°, 213.69°.

       
      This is a diagram of angles 33.69 degrees, 213.69 degrees, and negative 146.31 degrees in standard position.

      Source: Pre-Calculus 12. Whitby, ON: McGraw-Hill
      Ryerson, 2011. Reproduced with permission.



© 2012 Alberta Education