In Try This 2 you found the following is true for a point P(x, y) on the unit circle:
This information can be simplified to the following:
| cos θ = x | sin θ = y |
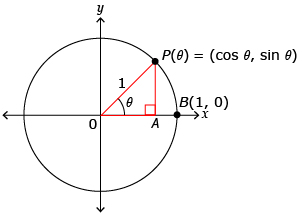
Source: Pre-Calculus 12. Whitby, ON: McGraw-Hill Ryerson, 2011.
Reproduced with permission.
So, you can write any point that lies on the unit circle at angle θ as P(θ) = (x, y) or P(θ) = (cos θ, sin θ).
Now that the relationship between a point P(x, y) and cos θ, sin θ, and tan θ has been identified, you can use this information to solve problems. An example of how to use the coordinates of a point on the unit circle to determine trigonometric ratios for an unknown angle follows.
Example: Determining Trigonometric Ratios Using a Point on the Unit Circle
The point P![]() lies on the unit circle at the intersection of a terminal arm of angle θ in standard position. Determine the values of sin θ, cos θ, and tan θ leaving the ratios as fractions.
lies on the unit circle at the intersection of a terminal arm of angle θ in standard position. Determine the values of sin θ, cos θ, and tan θ leaving the ratios as fractions.
Solution
Draw a diagram.
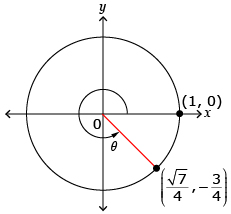
Point P is on the unit circle.
Determine cos θ. Since point P is on the unit circle, cos θ = x. The x-coordinate is, therefore, equal to cos θ.
![]()
Determine sin θ. Since point P is on the unit circle, sin θ = y. The y-coordinate is, therefore, equal to sin θ.
![]()
Determine tan θ.
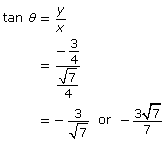
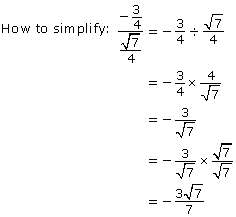
Self-Check 1
The point P![]() lies on the unit circle at the intersection of a terminal arm of angle θ in standard position.
lies on the unit circle at the intersection of a terminal arm of angle θ in standard position.
- Sketch a diagram of point P on the unit circle, and label angle θ in standard position. Answers
- Determine the values of sin θ, cos θ, and tan θ. Leave the ratios as fractions. Answers