Lesson 4: Trigonometric Ratios

 

Focus

 

Cycling is a great part of a healthy lifestyle and also contributes to a greener environment. Physical activity relieves stress by producing a balance between exertion and relaxation. The cyclical movement of the legs stimulates muscles in the lower back to strengthen the spine. The uniform, cyclical movement of cycling creates a considerable relaxing effect, which stabilizes the physical and emotional functions of the body.

 

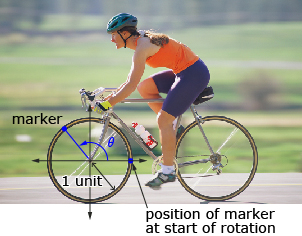
Take a closer look at this cyclical motion.

As you saw in Lesson 3, when choosing a radius of one unit for the wheel, the circumference of the wheel is 2π. When the outer edge of the wheel has travelled 2π, the wheel has gone through exactly one revolution, and so is back where it started. Thus, if a marker was placed on the wheel, you could look at the height and angle of rotation of the marker at specific times and relate these measures to points on the unit circle.

 

In Lesson 3 you derived the equation for the unit circle, and you determined the rotational angles in standard position and the coordinates of points where a terminal arm intersects the unit circle for specific angles.

 

In this Lesson you will discover how the unit circle can be related to trigonometric ratios.

Lesson Outcomes

 

At the end of this lesson you will be able to

• describe the six trigonometric ratios
• determine the exact value of trigonometric ratios for specific angles
• determine the approximate value of trigonometric ratios of any angle

Lesson Question

 

You will investigate the following question:

• How can the six trigonometric ratios be determined for any angle expressed in radians or degrees?

Assessment

 

Your assessment may be based on a combination of the following tasks:

• completion of the Lesson 4 Assignment (Download the Lesson 4 Assignment and save it in your course folder now.)
• course folder submissions from Try This and Share activities
• additions to Glossary Terms and Formula Sheet
• work under Project Connection