Historically, trigonometry was mostly used in astronomy and geography. The literal meaning of trigonometry is triangle measurement. In fact, the applications of trigonometry go far beyond geometry. For example, trigonometry also has applications in physics and music.

 

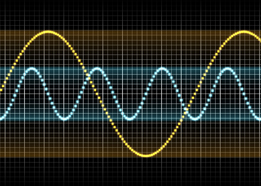
Many of the examples you will look at in Module 4 involve cyclic behaviour. Anything with a regular cycle (like tides, temperatures, pendulums, electric current, economics, or even riding a bicycle) can be modelled using a sine curve or a cosine curve to illustrate the pattern repeating itself. You can use your knowledge of trigonometry to develop sine and cosine graphs.

 

In this module you will investigate the following question:

• How can trigonometry be used to solve problems that involve cyclic behaviour?

To investigate this question you will focus on the lessons and questions in the table.

 

Lesson	Topic	Lesson Questions
1	Radians and Degrees in Standard Position	What relationship exists between degree and radian measures?
2	Applications of Radians	How can angles with the same terminal arms be described?
		How can the relationship between the central angle, arc length, and radius in a circle be used to solve real-life problems?
3	The Unit Circle	How is an equation of a circle derived?
		How are points on the unit circle determined?
4	Trigonometric Ratios	How can the six trigonometric ratios be determined for any angle expressed in radians or degrees?
5	Trigonometric Equations	How can trigonometric equations be solved?
		How is a specific solution for a trigonometric equation related to the general solution?
6	Graphing and Transforming Sine and Cosine Functions 1	How can the functions y = sin x and y = cos x be represented graphically?
		How do the parameters a and b of a trigonometric function affect the shape of the corresponding graph?
7	Graphing and Transforming Sine and Cosine Functions 2	How can the functions and be represented graphically?
		How are the parameters a, b, c, and d of a sine or cosine function related to the transformations of the corresponding graph?

 

Module 4 Project: The Ferris Wheel focuses on how trigonometry can be used to describe the repetition of an amusement park ride’s motion. When you look at the motion of a Ferris wheel, you can see the circular motion repeat with each rotation of the wheel.

 

You will be prompted to complete Module 4 Project: The Ferris Wheel as you work through the lessons. You might want to check the Module 4 Project for a sneak peek now.

Note: Loading times for video and other media may vary depending on your Internet connection. Please be patient.