In this module you investigated the following question: How can the ability to graph and analyze polynomial functions be used in graphic design?

 

In Module 3 Project: Graphic Design Using Polynomials, you looked at how you could use polynomial functions to model curves found in images and how the factors of the polynomial relate to the curve.

 

Two different, yet mathematically equivalent, forms of polynomial functions can be used to determine

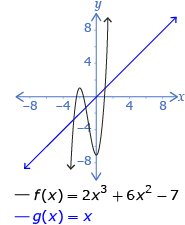
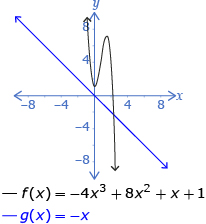
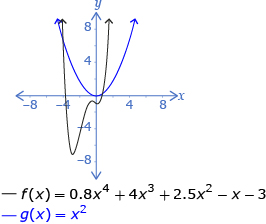
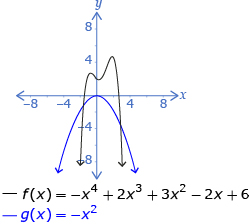
• end behavior of the function
• x-intercepts of the corresponding graph
• solutions to the corresponding equation

The following table summarizes the key ideas of the module.

 

Lesson 1	The end behaviour of a polynomial function can be determined by the degree and sign of the leading coefficient.	Odd-Degree, Positive-Leading Coefficient     Odd-Degree, Negative-Leading Coefficient       Even-Degree, Positive-Leading Coefficient       Even-Degree, Negative-Leading Coefficient
	The x-intercepts of a polynomial function can be determined by looking at the factors of the polynomial.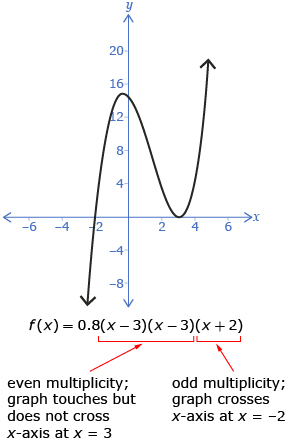
Lesson 2	You can perform long division on polynomials like you can with numbers.   Polynomials can be factored using the remainder theorem: (f(a) = the remainder when f(x) is divided by x − a) the factor theorem: look for values of a such that f(a) = 0 the integral zero theorem: try factors of the constant term of f(x);18 in the example shown
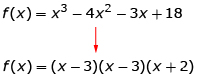Lesson 3	Polynomial equations can be solved by factoring polynomials and using the zero-product property.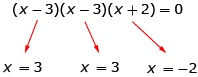