A lot of new information has been introduced in this lesson. Here is a summary of how the information fits together.
| Example | Mathematical Justification |
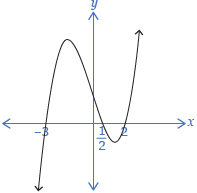
| In order to sketch f(x) = 2x3 + x2 – 13x + 6, you need to create an equivalent factored form. | The factors correspond to x-intercepts. |
Test for factors:
f(1) = −4
f(−1) = 18
f(2) = 0 x − 2 is a factor of f(x) because f(2) = 0. |
The remainder theorem tells you that f(a) = the remainder when f(x) is divided by x − a.
The factor theorem tells you to look for values of a such that f(a) = 0. The integral zero theorem tells you to try factors of the constant term of f(x). (In this example, 6.) |
 |
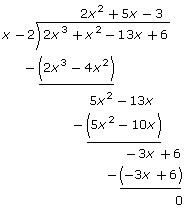Perform division to determine a second factor. |
| f(x) = (x − 2)(2x2 + 5x − 3) | This equivalent factored form can be written using f(x) = (x − a)Q(x) + R, where Q(x) is the quotient and R is the remainder. |
| f(x) = (x − 2)(x + 3)(2x − 1) | The equivalent factored form of 2x2 + 5x − 3 is (x + 3)(2x − 1). |
The graph of f(x) will have x-intercepts at 2, −3, and
|
These are the values that make each factor equal to zero, thus making f(x) = 0. |
Since f(x) is a cubic polynomial function with a positive leading coefficient, its graph will start in quadrant 3 and end in quadrant 1.