Module 2 Summary

 

In this module you used radical functions to model the relationships between distance, speed, and time for objects as they accelerate. You saw this in objects dropped or thrown, tire skid marks from a vehicle, and the swinging of a pendulum. These relationships were graphed and solved using radical functions.

 

This is a collage of photographs. The collage includes a clock with a pendulum that moves back and forth, a lacrosse stick and ball, and skid marks on a road.
clock: © asky/2192348/Fotolia; lacross: Hemera/Thinkstock; road: iStockphoto/Thinkstock



You investigated the following question:

You learned how to sketch the graphs of radical functions using your knowledge of transformations from Module 1. The sketches of the graphs of radical functions were made by using the form and by transforming the function . You also identified the domain and range of the radical functions.

 

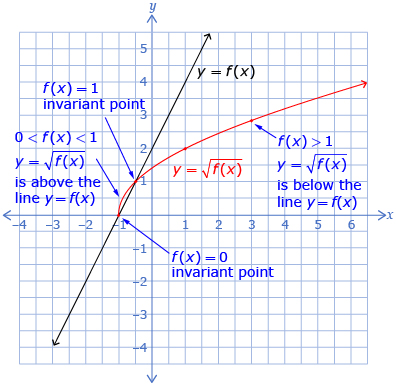
You learned how to sketch the graph of when given the graph of the function y = f(x). To do this, you used key points and the understanding that the y-coordinates of the function are the square root of the y-coordinates of the function y = f(x). You also compared the domain and range of each function and explained why the domain and range might be different.

 

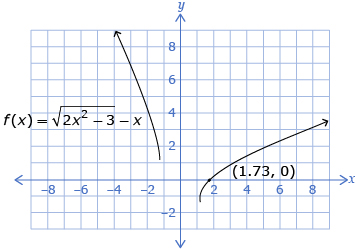
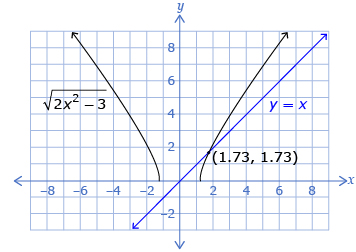
A graphical method was used to solve radical equations. Two methods were studied. One method used a graph of a single function, and the solution was the value of the x-intercept(s). The other method used the graphs of a system of two functions, and the solution was the x-value of the point(s) of intersection.

 

In Module 2 Project: Pendulums, you applied what you learned in this module to study the relationship between the period and length of a pendulum. You graphed and determined the equation for the function, and you described the transformations of the new function from the base function. You used this equation to determine graphically the period of a pendulum with a given length. You used a graph of a square root of a given function to determine the velocity of a pendulum.

 

Following are some of the key ideas that you learned in each lesson.

 

Lesson 1

Sketch the graph of  by applying transformations to the graph of the function

  • a is the vertical stretch by a factor of |a| about the x-axis, if a < 0, a reflection across the x-axis.
  • b is the horizontal stretch by a factor of  about the y-axis, if b < 0, a reflection across the y-axis.
  • h is the horizontal translation by h units.
  • k is the vertical translation (k units).
Lesson 2

Sketch the graph of when given the graph of the function y = f(x).

  • Invariant points of the two graphs are when f(x) = 0 and f(x) = 1.
  • The y-coordinates on the graph of are the square roots of the y-coordinates on the original function y = f(x).

    This shows the graph of two functions. This first function is y equals x plus 4, which is a straight line. The second is y equals begin square root of x plus 4 end square root, which is a half parabola opening to the right. The invariant points are labelled at (negative 1, 0) and (negative 0.5, 1). The graph of y equals square root of f at x is above the line y equals f at x when the y values are from zero to one. The square root function is below the line y equals f at x when the y values are greater than one.
Lesson 3

To solve radical equations graphically, you can use one of two methods to determine the solution.

  • Graph a single function and determine the x-intercept(s). The solution of the equation is x ≈ 1.73.

    This graphic shows the two curved lines making up the graph of y equals begin square root 2 times x squared minus 3 end square root minus x. The graph crosses the x-axis at (1.73, 0).
  • Graph a system of two functions and determine the x-value of the intersection point(s). The solution of the equation is x ≈ 1.73.

    This is a graph of two functions. One function has two curved lines and is y equals begin square root 2 times x squared minus 3 end square root. The other function is a straight line and is y equals x. The intersection point between the two functions is labelled (1.73, 1.73).