Pendulums
Project Overview
Purpose
In this project you will relate and explain the concepts from Module 2 to the pendulum.
Process
Towards the end of each lesson, under Project Connection, you may be prompted to complete a part of the Module 2 Project. You can access the entire project from this page at any time.
Make sure to save all work from each Project Connection in your course folder. You will submit your entire Module 2 Project to your teacher at the end of Module 2. Check with your teacher about how you should submit your project work before you begin the project.
Presentation
The most important part of your project presentation is clearly explaining and supporting your reasoning with relevant visuals and calculations. Make sure to show all your work.
You can choose any format you prefer for the final presentation of this project. Some options include a written document, virtual or real poster, website, video, oral report, or slideshow presentation.
Materials and Equipment
You will need the following supplies:
- thread
- washers or other suitable mass
- tape
- ruler
- stopwatch or timer
- graph paper
Project Introduction
Hemera/ThinkstockA simple pendulum consists of an object hung by a string from a fixed support. The object typically hangs vertically in its equilibrium position. The object is referred to as the pendulum bob. When the bob is pulled back and then released, it begins its back-and-forth motion. The motion is regular and repeating; an example of periodic or harmonic motion.
Watch an example of many pendulums swinging at different lengths in the video “Pendulum Waves.”
Copyright 2011 President and Fellows Harvard College. All Rights Reserved. Reproduced with permission.
Pendulums are found in many places. A child swinging on a playground swing forms a pendulum, as do some amusement park rides. Some clocks have pendulums to help keep accurate time. The first pendulum clock was made by the Dutch scientist Christian Huygen in 1656.
Part 1: Transformation of a Radical Function
Have you ever tried bungee jumping? After the elastic cord used in bungee jumping has stopped stretching and compressing, the person at the bottom of the cable is left swinging back and forth—somewhat like a pendulum.
Hemera/Thinkstock
In this project you will investigate some properties of pendulums and see how pendulums relate to radical functions. Respond to the following questions.
- Where do people bungee jump? Investigate some locations of bungee jumping, and describe one location you find.
- To understand some of the properties of pendulum motion, conduct an investigation. Complete question 18, including all steps, on page 76 of the textbook.
Save your responses in your course folder. Then return to Lesson 1.
Part 2: Square Root of a Function
liquidlibrary/Thinkstock
This act involves a performer or “flyer" using a trapeze and jumping from a platform set high above the ground in order to create a swinging motion.
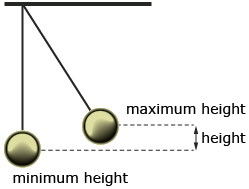
The motion of a person performing on the flying trapeze resembles that of a pendulum and is called simple harmonic motion. There is a constant transfer of energy as the trapeze artist makes his or her way through one swing. By moving her or his body, the performer can vary the length of the pendulum and, therefore, change the period of the swing. An acute awareness of position and speed of the swing is critical to the performer.
Knowing the difference in height between the highest point of the swing of the pendulum and the lowest point, you can approximate the speed the mass at the end of a pendulum is moving.
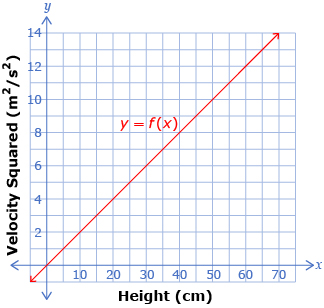
A student studied the pendulum motion of the flying trapeze. The student graphed the velocity squared of the performer at the lowest point of the swing as a function of the difference in height between the highest and lowest points on the path of the pendulum. The following graph shows the velocity squared, v2, in m2/s2 as a function of height, h, in centimetres.
- Use the function y = f(x) shown in the preceding graphic, and sketch the graph of
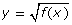. Explain the process you used.
- Compare the domain and range of y = f(x) and
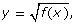and explain why the domains and ranges may be different.
- Choose a height for your pendulum. Use the graph you created of
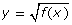to determine the velocity for your chosen height.
Save your responses in your course folder. Then return to Lesson 2.
Part 3: Solving a Radical Equation
- Using the equation you determined from Part 1, graphically solve for the length of the pendulum when the period of the pendulum is 2.0 s. Make sure to round your answer to the nearest tenth of a centimetre.
- After a person has completed a bungee jump and the bungee cord has stopped stretching and compressing, the person could swing back and forth like a pendulum. The person does not want to swing back and forth too quickly, so the period should be 12 s.
- Use your equation for a pendulum from Part 1 of the project to determine the length of a pendulum if the period is 12 s. Remember that, in your equation, the length is in centimetres. Make sure to round your answer to the nearest whole centimetre.
- Would the place that you researched for a bungee jump in question 1 of Part 1 work with a 12-s period? Why or why not?
Save your responses in your course folder.
Conclusion
Write a brief conclusion to your Module 2 Project. Include a personal reflection of what you learned from the project during and after completion. Be sure to explain why you felt the way you did.
Save your conclusion in your course folder. Then return to Lesson 3.
Project Assessment
Your Module 2 Project will be evaluated by your teacher using the evaluation guidelines in the project rubric. Read the rubric carefully. Make sure you are aware how you will be assessed. You can print or save a digital copy of the Module 2 Project Rubric as a guide to help you complete your project.
Don’t forget to submit your completed Module 2 Project to your teacher at the end of Module 2.
