Module 2: Radical Functions

 

Explore

 

In Try This 1 you compared the graphs of y = x + 4 and You may have noticed that the mapping  shows the correspondence between points on the first graph and those points on the second graph.

 

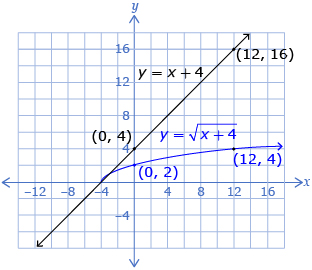
This graphic shows the graphs of two functions. The first is y equals x plus 4 as a straight line. The second is the function y equals the beginning of the square root x plus 4 end square root as a half parabola opening to the right. The points (0, 4) and (12, 16) are labeled on the linear graph. The corresponding points (0, 2) and (12, 4) are labeled on the graph of the square root function.

What other patterns do you see when you compare the original function y = x + 4 and the square root of the original function

 

In Try This 2 you will compare a given function to the square root of the given function.

 

Try This 2

 

Use Visualizing Square Root to compare a function f(x) and the square root of that function

 

 

This play button opens Visualizing Square Root.

 

Comparison 1 has been done for you as an example.

 

Comparison 1: Compare the functions f(x) = −x + 1 and

 

Step 1: Select the linear function in Visualizing Square Root.

 

Step 2: Use the sliders to set a to −1 and b to 1.

 

Step 3: Select the "Show Square Root" box and compare the two graphs. Record your observations in a table.

 

Solution

 

  f(x) = –x + 1
Domain {x|x ∈ R} {x|x ≤ 1, x ∈ R}
Range {y|y ∈ R} {y|y ≥ 0, y ∈ R}
Invariant Point(s) (1, 0) and (0, 1)
Sketch/Image of Both Functions 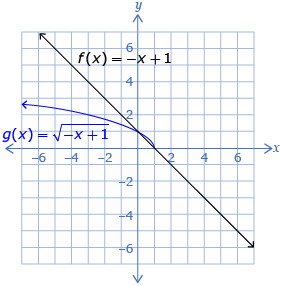This is a graph of two functions. One function is a linear function, f at x equals negative x plus 1. The other function is a radical function, g at x equals the beginning of square root negative x plus 1 end square root. Both functions fall from the upper right and pass through (0, 1) and (1, 0). The radical function is the upper half of a parabola with a vertex at (1, 0).

 

Comparison 2: Compare the functions f(x) = 0.5x − 1 and


Step 1: Change a to 0.5 and b to −1.


Step 2: Record your observations in a table similar to the following one.

 

  f(x) = 0.5x − 1
Domain    
Range    
Invariant Point(s)  
Sketch/Image of Both Functions  

 

Comparison 3: Compare the functions f(x) = x2 − 1 and


Step 1: Change the function to quadratic.


Step 2: Change a to 1, h to 0, and k to −1.


Step 3: Record your observations in a table similar to the following one.

 

  f(x) = x2 − 1
Domain    
Range    
Invariant Point(s)
Sketch/Image of Both Functions  

 

Comparison 4: Compare the functions f(x) = 3x2 + 4 and


Step 1: Change a to 3, h to 0, and k to 4.


Step 2: Record your observations in a similar table.

 

  f(x) = 3x2 + 4
Domain    
Range    
Invariant Point(s)  
Sketch/Image of Both Functions  
  1. Look at the location of the invariant points. Is there a pattern? Why are the invariant points located where they are?
  2. How do the domains compare? Why are there differences?
  3. How do the ranges compare? Explain the differences.
  4. Refer to the sketches of each comparison. What happens to the value of 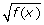as the value of f(x) changes? Use the following table to summarize the common patterns you observed for all four comparisons.

    Value of f(x)

    (original graph)

    When the y values are less than 0

    (f(x) < 0)

    When the y value is 0

    (f(x) = 0)

    When the y values are between 0 and 1

    (0 < f(x) < 1)

    When the y value is 1

    (f(x) = 1)

    When the y values are greater than 1

    (f(x) > 1)
    Value of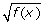          

course folder Save your responses in your course folder.

 

Share 2

 

With a partner or group, discuss the following questions based on your graphs created in Try This 2:

 

Based on the patterns you identified in Try This 2, create a method you could use to graph the square root of any function.

 

course folder If required, save a record of your discussion in your course folder.

An invariant point is a point on a graph that remains the same after a transformation is applied to the graph.

There are four invariant points. Two of the points are approximately (1.4, 1) and (−1.4, 1).