Module 1 Summary

 

Look at the pictures again from the module introduction. What transformations do you see? If you look closely you can see translations, stretches, and reflections as well as some other transformations. Transformations make it possible to manipulate functions in a variety of interesting ways, as seen in these and other pieces of art.

 

This is a picture of cubes of different sizes stacked in a pattern. This middle diagram shows many coloured hexagons of decreasing size spiraling inward. This picture on the right shows what appears to be a cube, but perspective is not consistent and the picture can be interpreted in different ways.

first image: © fat*fa*tin/4816771/Fotolia; second image: © pureguitarfury/6053388/Fotolia;
third image: Hemera/Thinkstock



In this module you investigated the following questions:

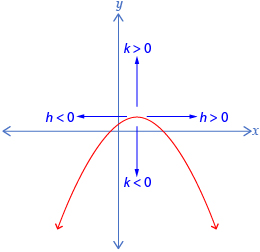
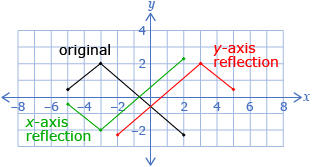
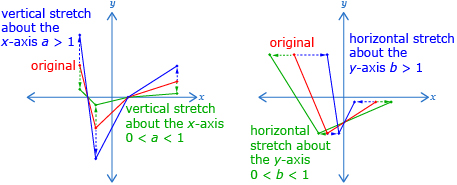
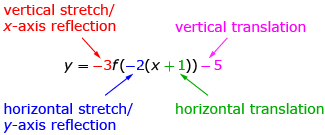
You learned to transform a function in a variety of ways. Most of these transformations can be represented using the equation y = af(b(x − h)) + k. Starting with f(x), changing a caused a vertical stretch by a factor of a and a reflection across the x-axis if a was negative. Changing b caused a horizontal stretch by a factor of  and a reflection across the y-axis if b was negative. The h-value translated the graph right h units (left if h is negative). Adding a k-value caused a vertical transition up k units (down if k is negative).

 

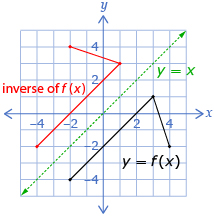
You also learned how to determine the inverse of a function, both graphically and by using equations. The inverse of f −1(x) “undoes” f(x).

 

In the Module 1 Project you transformed functions to design an image. You saw how a single function can be changed in many ways depending on the different transformations applied to the function.

 

Following are some of the key ideas that you learned in each lesson.

 

Lesson 1

Translations of Functions of the Form y – k = f(x – h)

 

The diagram shows a parabola opening down on a coordinate grid. Four arrows point from the parabola. The arrow pointing up is labelled k > 0, the arrow pointing down is labelled k < 0, the arrow pointing left is labelled h < 0, and the arrow pointing right is labelled h > 0.
Lesson 2

Reflections of Functions Across the x-axis and y-axis

 

This diagram shows a function labelled Original, its reflection across the y-axis labelled y-axis reflection, and its reflection across the x-axis labelled x-axis reflection.
Lesson 3

Stretches of Functions of the Form y = af(bx)

 

This diagram shows two functions being stretched. The first diagram shows a vertical stretch about the x-axis and the figure appears taller if a > 1 and shorter if 0 < a < 1. The second diagram shows a horizontal stretch about the y-axis and the figure appears wider if 0 < b < 1 and narrower if b > 1.
Lesson 4

Transformations of Functions of the Form y = af[b(x – h)] + k

 

This diagram shows y = –3f(–2(x + 1)) – 5. The –3 is labelled Vertical Stretch, the –2 is labelled Horizontal Stretch, the +1 is labelled Horizontal Translation, and the –5 is labelled Vertical Translation.
Lesson 5

Inverse of Function—Reflection of Functions Across the Line y = x

 

This diagram shows that a function and its inverse are reflections of each other across the line y = x.